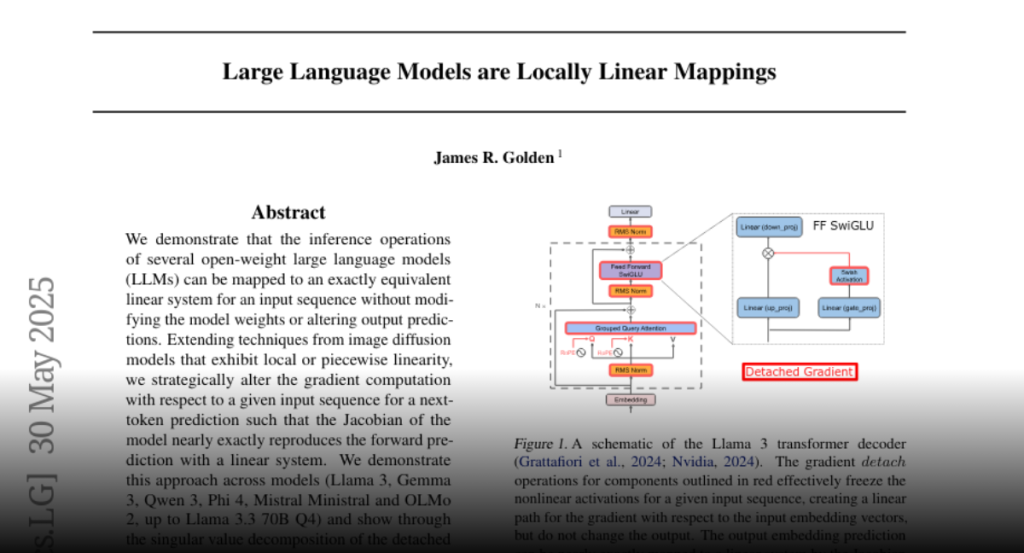
LLMs are nonlinear functions that map a sequence of input embedding vectors to a predicted embedding vector. We show that despite this, several open-weight models are locally linear for a given input sequence, which means that we can compute a set of linear operators (the “detached Jacobian”) for the input embedding vectors such that they nearly exactly reconstruct the predicted output embedding. This is possible due to a linear path through the transformer decoder (e.g., SiLU(x) = x*sigmoid(x) is locally or adaptively linear if you freeze the sigmoid term) which requires zero-bias linear layers.
This offers an alternative and complementary approach to interpretability at the level of single-token prediction. The singular vectors of the detached Jacobian can be decoded with the output tokenizer to reveal the semantic concepts that the model is using to operate on the input sequence. The decoded concepts are relevant to the input tokens and potential output tokens, and the different singular vectors often encode distinct concepts. This approach also works for the output of each layer, so the semantic representation can be decoded to observe how concepts form deeper in the network.
We also show the detached Jacobian can be used as a steering operator to insert semantic concepts into next token prediction.
This is a straightforward way to do interpretation that exactly captures all nonlinear operations (for a particular input sequence). There is no need to train a separate interpretability model, it works across Llama 3, Gemma 3, Qwen 3, Phi 4, Mistral Ministral and OLMo 2 models, and could have utility for safety and bias reduction in model responses. The tradeoff is that the detached Jacobian must be computed for every input sequence.
Attached is a figure demonstrating local linearity in Deepseek R1 0528 Qwen 3 8B at float 16 precision. The demo notebooks for Llama 3.2 3B and Gemma 3 4B can run on a free T4 instance on colab.